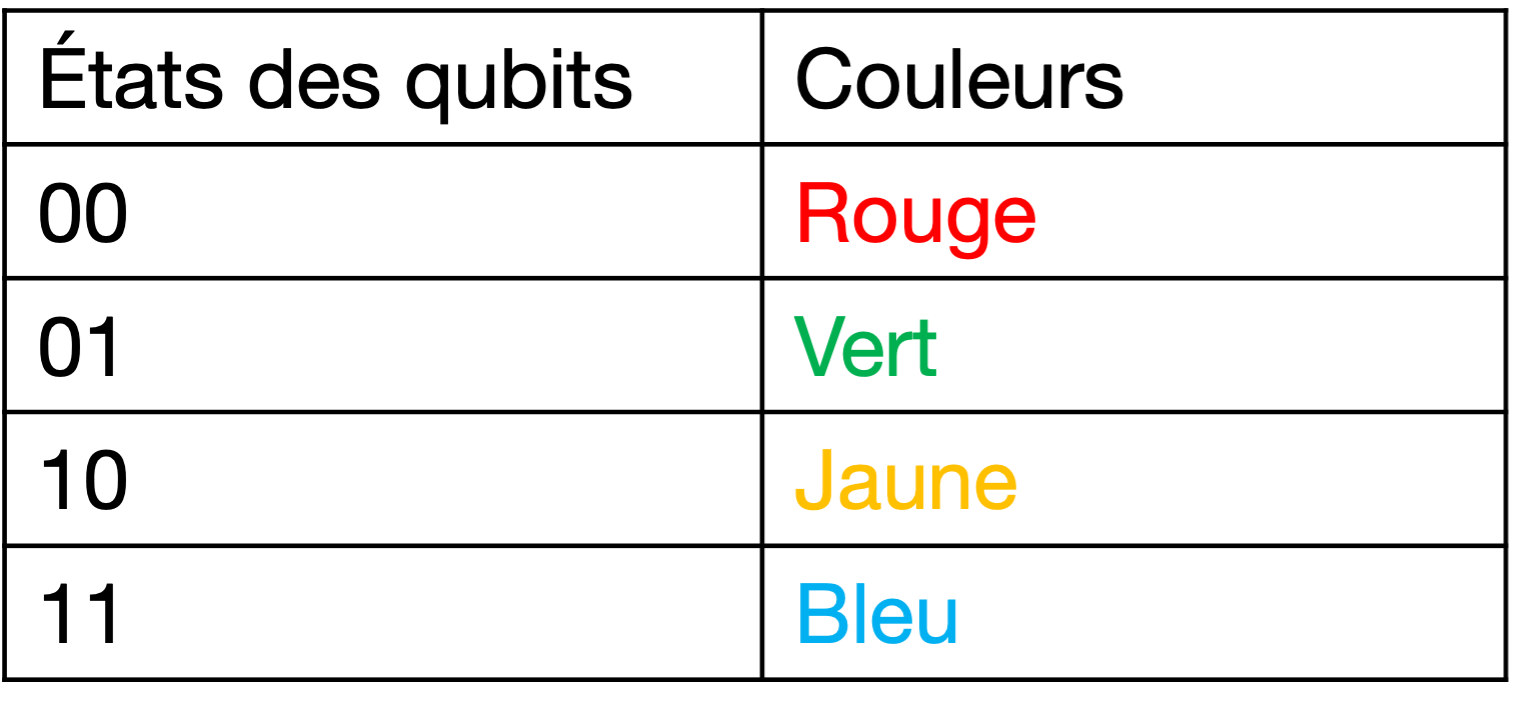Résoudre un problème d’optimisation avec l’ordinateur quantique

Par Aiky Rasolomanana, stagiaire à l’Espace IBM Quantique de l’IQ
Avec la participation de Maxime Dion, développeur en informatique quantique à l’Espace IBM Quantique de l’IQ

Un graphe est un ensemble de points, appelés sommets, qui peuvent être connectés entre eux par des segments, appelés arêtes. Ce mot peut sembler abstrait pour certains ou constituer une monstruosité mathématique pour d’autres. Qu’on le veuille ou non, les graphes sont omniprésents et leurs applications sont bien réelles dans plusieurs domaines tels que l’informatique, la finance, ou encore la pharmacologie.

Les graphes et le problème du coloriage

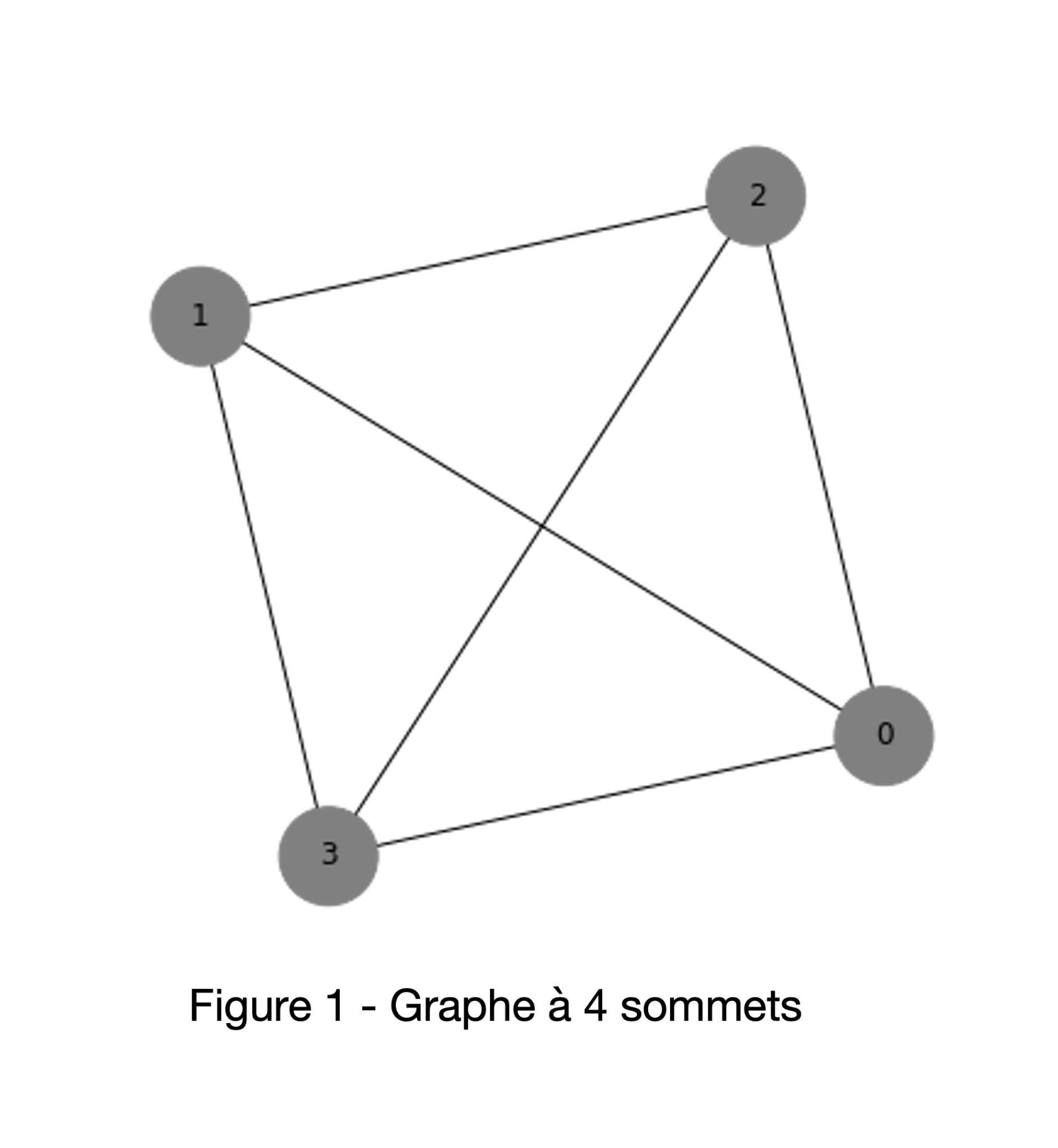
Un défi bien connu dans la théorie des graphes consiste à en colorier les sommets en utilisant un nombre donné de couleurs tout en s’assurant que les paires de sommets connectés ne soient jamais de la même couleur. Dans cet article, nous tenterons de colorier un graphe illustré dans la figure 1 avec quatres couleurs différentes. Bien que ce problème puisse paraître trivial, le développement d’une méthode de solution efficace pouvant être utilisée sur des graphes de plus grandes tailles, pourrait permettre de résoudre des problèmes beaucoup plus complexes ayant des applications bien concrètes. 
 
En pratique, pour résoudre le problème du coloriage, une méthode consiste à essayer toutes les configurations possibles, une par une, jusqu’à ce qu’une d’entre elles respecte la contrainte du départ. Ici, on postule qu’il y a une solution possible. Cette méthode nécessite d’essayer un nombre de configurations qui croit exponentiellement avec le nombre de sommets à colorier et est impraticable pour des graphes de grande taille.

Le coût 

Avant de chercher à résoudre quoique ce soit, il convient d’intégrer un élément fondamental à la résolution d’un problème d’optimisation de ce genre : le coût.
L’idée est la suivante : on attribue à chaque arête une valeur, 1 si les sommets qu’elle relie sont de la même couleur et 0 dans le cas opposé. La somme des valeurs pour toutes les arêtes définit une valeur globale, le coût. Le problème revient alors à trouver une configuration qui minimise ce coût.

Un algorithme hybride (quantique/classique)

Avec le développement actuel de l’ordinateur quantique, on peut explorer une méthode pour résoudre le problème du coloriage. Dans le cas présent, on associe 2 qubits à chacun des 4 sommets pour un total de 8 qubits. Les 4 états de base de chacune des paires de qubits peuvent alors être associés aux 4 couleurs comme dans le tableau 1 dessous: 

L’état quantique du système de 8 qubits peut alors exploiter les phénomènes de superposition et d’intrication pour représenter en même temps plusieurs coloriages du graphe. On peut ainsi « tester » simultanément un nombre exponentiellement grand de configurations.

Typiquement, l’état quantique est préparé par un circuit quantique où certaines portes quantiques peuvent être ajustées grâce à des paramètres. On nomme Ansatz la forme arbitraire de ce circuit quantique. La mesure des qubits permet ensuite d’évaluer le coût moyen associé à tous les coloriages qui sont inclus dans l’état quantique.

Dans le cadre d’un algorithme hybride, un ensemble de paramètres initiaux est utilisé pour préparer un premier état quantique dans l’ordinateur quantique. Les qubits sont mesurés et le coût moyen est évalué. De son côté, l’ordinateur classique détermine ensuite un second ensemble de paramètres, en variant légèrement les paramètres précédents, qui seront utilisés pour faire une nouvelle évaluation du coût. Si celui-ci diminue, l’algorithme classique va continuer à varier les paramètres comme précédemment, sinon il cherchera un autre ensemble de paramètres qui permet une diminution du coût.

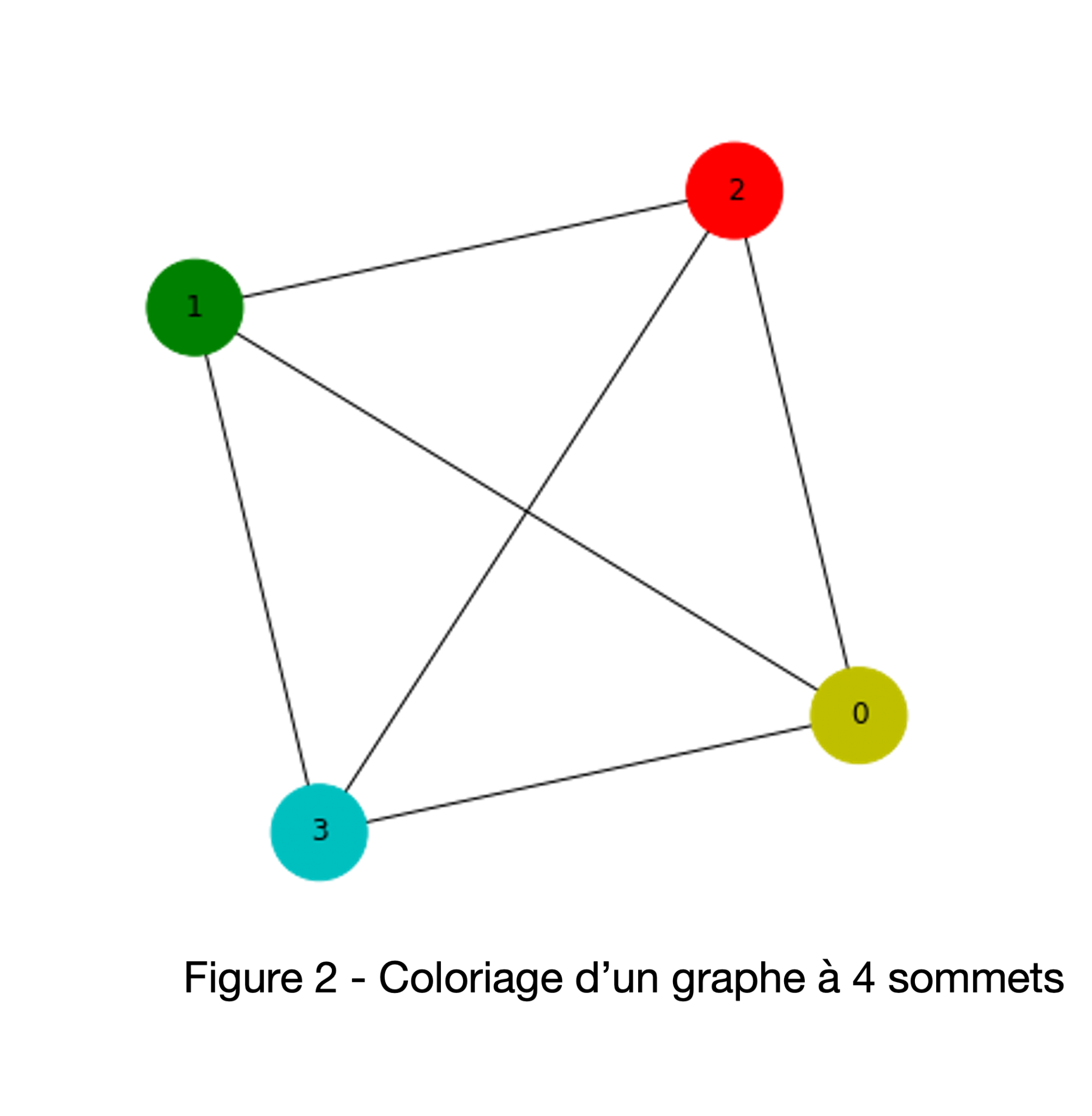
Ce processus est répété jusqu’à ce que l’algorithme converge vers un minimum qu’on espère absolu. Une fois cette boucle terminée, les qubits sont mesurés afin d’obtenir l’état du système. L’état de base qui a la plus grande probabilité d’être mesuré est converti en couleurs et celles-ci sont appliquées au graphe pour obtenir la solution au problème posé, comme à la figure 2. Cette méthode hybride porte le nom d’Algorithme d’Optimisation Quantique Approximative (QAOA).

Des problèmes variés et complexes 

Le problème du coloriage fait partie d’une classe de problèmes dits d’optimisation. Ainsi, on peut adapter l’algorithme présenté ici pour traiter d’autres problèmes d’optimisation comme la création d’un horaire plus efficace pour chaque avion d’une compagnie aérienne.

Si résoudre un système avec quelques sommets n’impressionne pas tout le monde, il faut reconnaître qu’à l’heure actuelle, les ordinateurs quantiques ont certaines limites qui empêchent la résolution de systèmes plus complexes ou de plus grande taille. Mais à mesure que la technologie progressera, on peut imaginer un futur dans lequel l’ordinateur quantique permettra de résoudre des problèmes qui sont hors de portée pour nos ordinateurs actuels.