Atténuation des erreurs sur la mesure des qubits
Par Connor Doonan, Stagiaire à l’Espace IBM Q de l’Institut quantique
Avec la participation de Maxime Dion, Développeur en informatique quantique à l’Espace IBM Q de l’Institut quantique
La prolifération d’erreurs lors de l’exécution d’un circuit quantique est l’un des principaux défis de l’informatique quantique. Que ce soit des signaux qui disparaissent ou des erreurs de lecture, les systèmes quantiques actuels ne sont pas encore parfaits. Plutôt que de consacrer temps et énergie à fabriquer un ordinateur quantique infaillible, il est plus judicieux de minimiser l’impact de ces erreurs en utilisant l’atténuation d’erreur. Lorsqu’on parvient à comprendre les erreurs produites par un système, il devient possible d’arriver à les détecter pour ensuite limiter leur impact, voir même les corriger.
Dans cette réflexion quantique, nous nous intéresserons spécifiquement à l’atténuation des erreurs produites lors de la mesure de l’état des qubits. Étant donné la nature statistique de plusieurs types de calculs quantiques, les erreurs engendrées lors de la mesure des qubits peuvent être statistiquement atténuées. Par exemple, si un qubit semble être mesuré dans l’état 0 plus souvent qu’il ne le devrait, on peut artificiellement changer quelques 0 pour des 1 afin d’obtenir un résultat plus précis.
Durant mon stage au printemps 2021 à l’Espace IBM Q de l’Université de Sherbrooke, j’ai eu la chance d’expérimenter deux méthodes d’atténuation d’erreurs de mesure des qubits : les calibrations complètes et les calibrations tensorielles des bases de mesure.
Calibration complète de la base de mesure
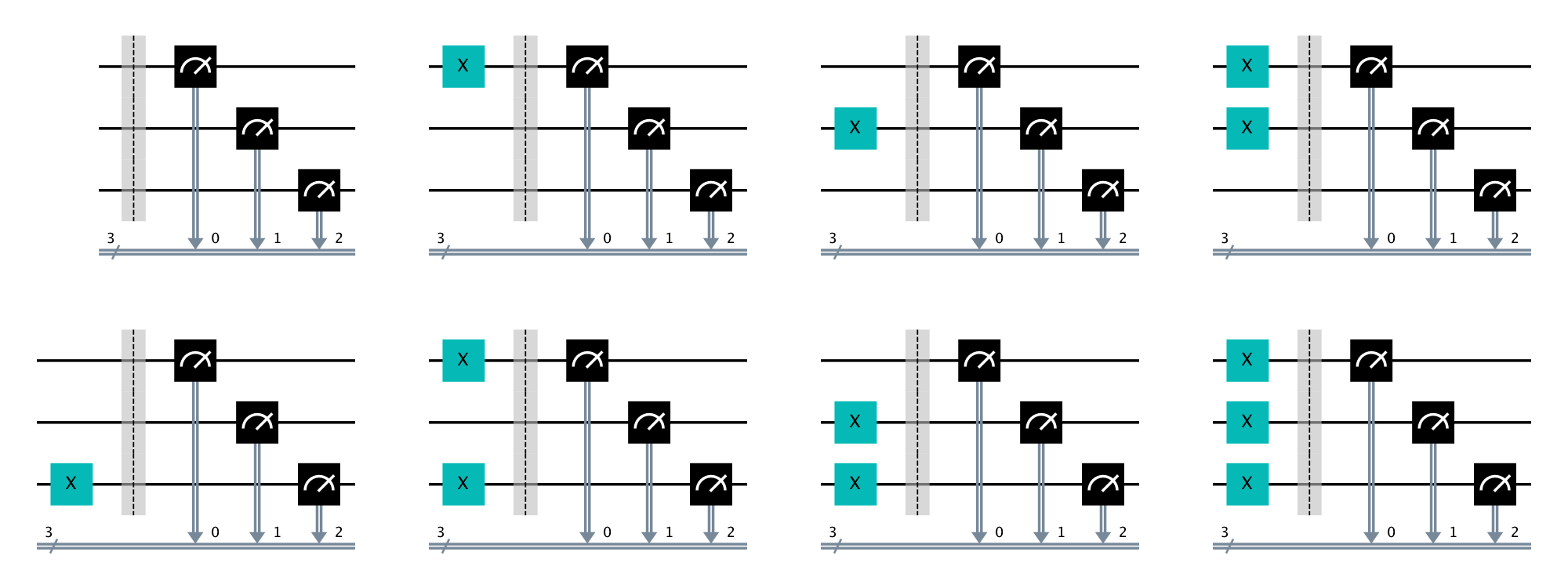
La calibration complète d’un système de n qubits débute par la génération d’une série de circuits quantiques qui serviront à préparer les qubits dans les 2n états de base et de les mesurer. Par exemple, la figure 1 illustre les circuits nécessaires pour calibrer un système de trois qubits (23=8). Chacun des circuits doit alors être exécuté un grand nombre de fois pour accumuler des statistiques sur le comportement des qubits.
Figure 1
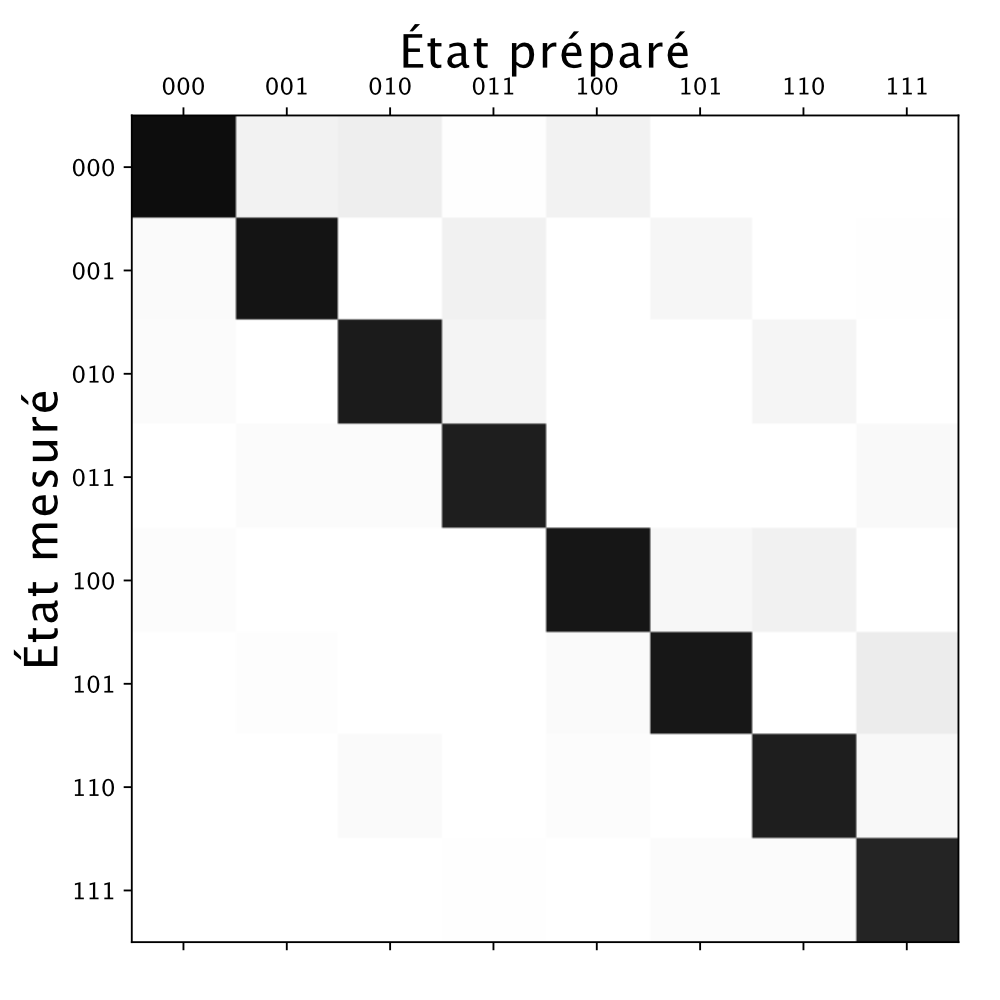
Pour la plupart des exécutions, l’état mesuré est bien l’état préparé, à moins qu’une erreur ne se soit produite. Cela permet de construire la matrice de calibration complète en compilant le nombre de fois que chacun des états de base a été obtenu lors de la préparation d’un des états de base, comme le montre la figure 2.
Figure 2
Si les qubits étaient parfaits, cette matrice serait diagonale. Sans entrer dans les détails, les méthodes d’atténuation des erreurs sur la mesure des qubits passe par la construction d’un filtre qui permet de transformer cette matrice de calibration vers une matrice diagonale. Le filtre ainsi créé peut ensuite être appliqué sur les résultats de n’importe quel calcul quantique pour obtenir une réponse plus précise.
La mise en place de cette méthode comporte cependant un obstacle de taille : elle requiert l’exécution d’un nombre exponentiel de circuits quantiques et la construction d’une matrice exponentiellement grande. Cela devient rapidement impossible en pratique même pour des systèmes de taille modeste, comme ceux que l’on connait actuellement.
Calibration tensorielle de la base de mesure
C’est ici que la calibration tensorielle de la base d’état entre en jeu. Au lieu de préparer tous les états de base du système, on génère les matrices de calibration pour des sous-ensembles de quelques qubits qui couvrent l’entièreté du système. Cette méthode suppose cependant que les erreurs qui se produisent dans ces sous-groupes sont indépendantes.
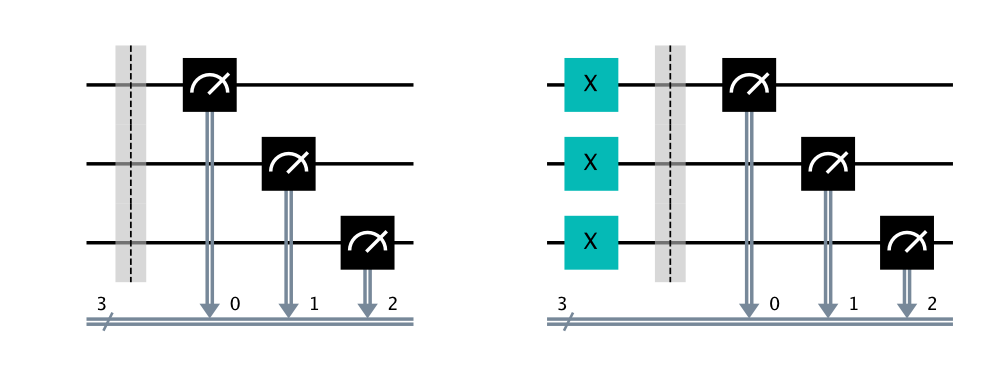
On peut combiner les circuits agissant sur les différents sous-groupes pour les exécuter en parallèle. Cette façon de faire permet de réduire drastiquement le nombre de circuits quantiques nécessaires. En particulier, si on forme des sous-groupes comportant chacun un seul qubit, on peut calibrer l’ensemble du système à l’aide de seulement deux circuits quantiques. La figure 3 montre les deux circuits qui permettent de calibrer notre système de trois qubits en utilisant la méthode tensorielle.
Figure 3
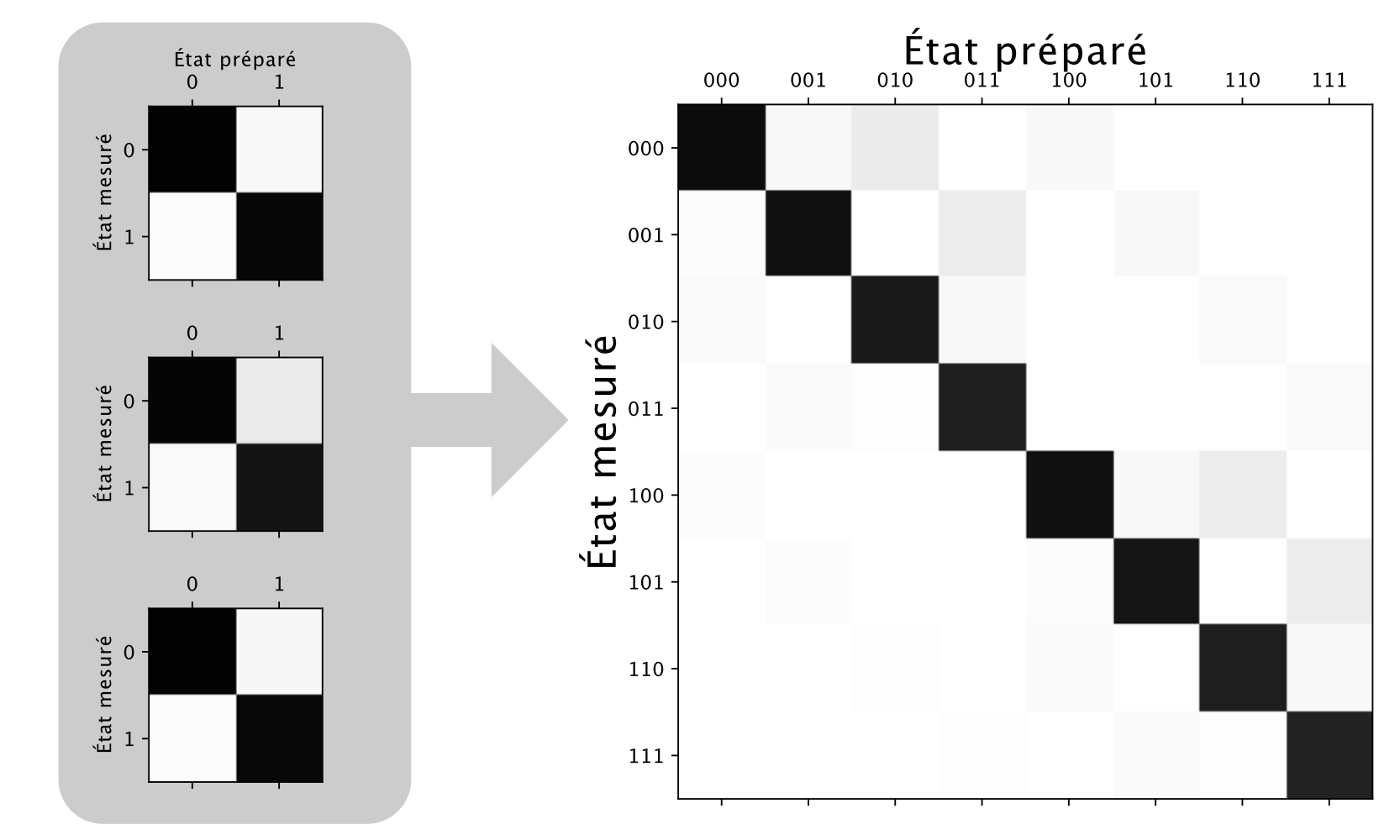
Après l’exécution de ces circuits, on peut construire les matrices de calibration pour chacun des qubits. Le produit tensoriel permet de reconstruire une approximation de la matrice de calibration complète, comme le montre la figure 4. En pratique, cette matrice n’est pas calculée : c’est justement ce qu’on cherche à éviter!
Figure 4
Une comparaison rapide des figures 2 et 4 révèle quelques différences mineures, ce qui suggère que les erreurs se produisant sur différents qubits pourraient être reliées. Néanmoins, les similitudes montrent que cela reste une bonne approximation, en particulier lorsque l’on tient compte du coût en ressources entre les deux méthodes.
IBM Quantum caractérise les erreurs de mesure pour chacun des qubits régulièrement sur ses systèmes. Les données pour construire les matrices de calibration de chaque qubit sont donc déjà disponibles pour mettre en place la méthode tensorielle pour des qubits uniques. Il est même possible de récupérer les calibrations pour des dates antérieures, permettant d’appliquer l’atténuation des erreurs de mesure sur des calculs effectués dans le passé.
Résultats des différentes méthodes
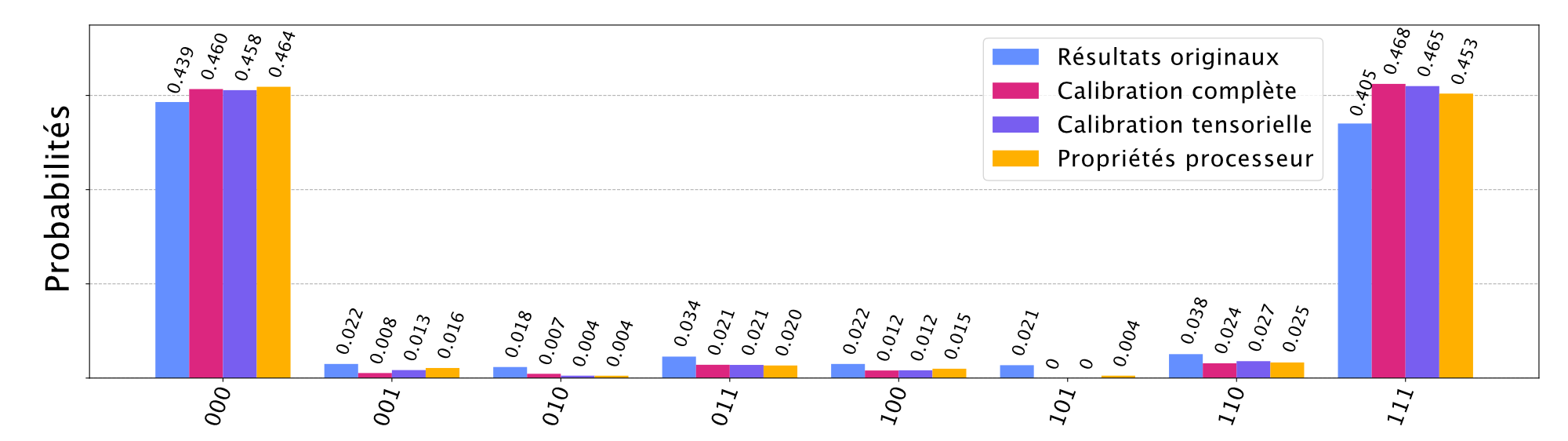
Une question demeure : Comment comparer les résultats obtenus par chacune des méthodes? Pour y répondre, nous appliquons ces méthodes à la préparation et la mesure d’un état GHZ à trois qubits. La figure 5 résume les résultats pour les méthodes et les compare aux résultats originaux en plus de la comparaison avec les valeurs fournies par IBM Quantum. Bien que la méthode de calibration complète semble offrir de meilleures performances, les deux autres méthodes permettent des améliorations intéressantes tout en utilisant beaucoup moins de ressources.
Figure 5
Bien entendu, aucune de ces méthodes ne permet de compenser parfaitement les erreurs de mesure des qubits. De plus, les résultats obtenus sont également affectés par d’autre types d’erreurs qui surgissent lors de l’application des portes quantiques ou juste avec le temps qui passe. Pour gérer ces erreurs les méthodes dites de correction d’erreurs sont nécessaires et feront l’objet d’une future réflexion quantique.