La Polarisation, c’est naturellement quantique

Par Sarah Blanchette et Maxime Dion 

Dans cette réflexion quantique nous verrons que la superposition quantique se manifeste très naturellement dans une propriété de la lumière :  sa polarisation.

Polarisation

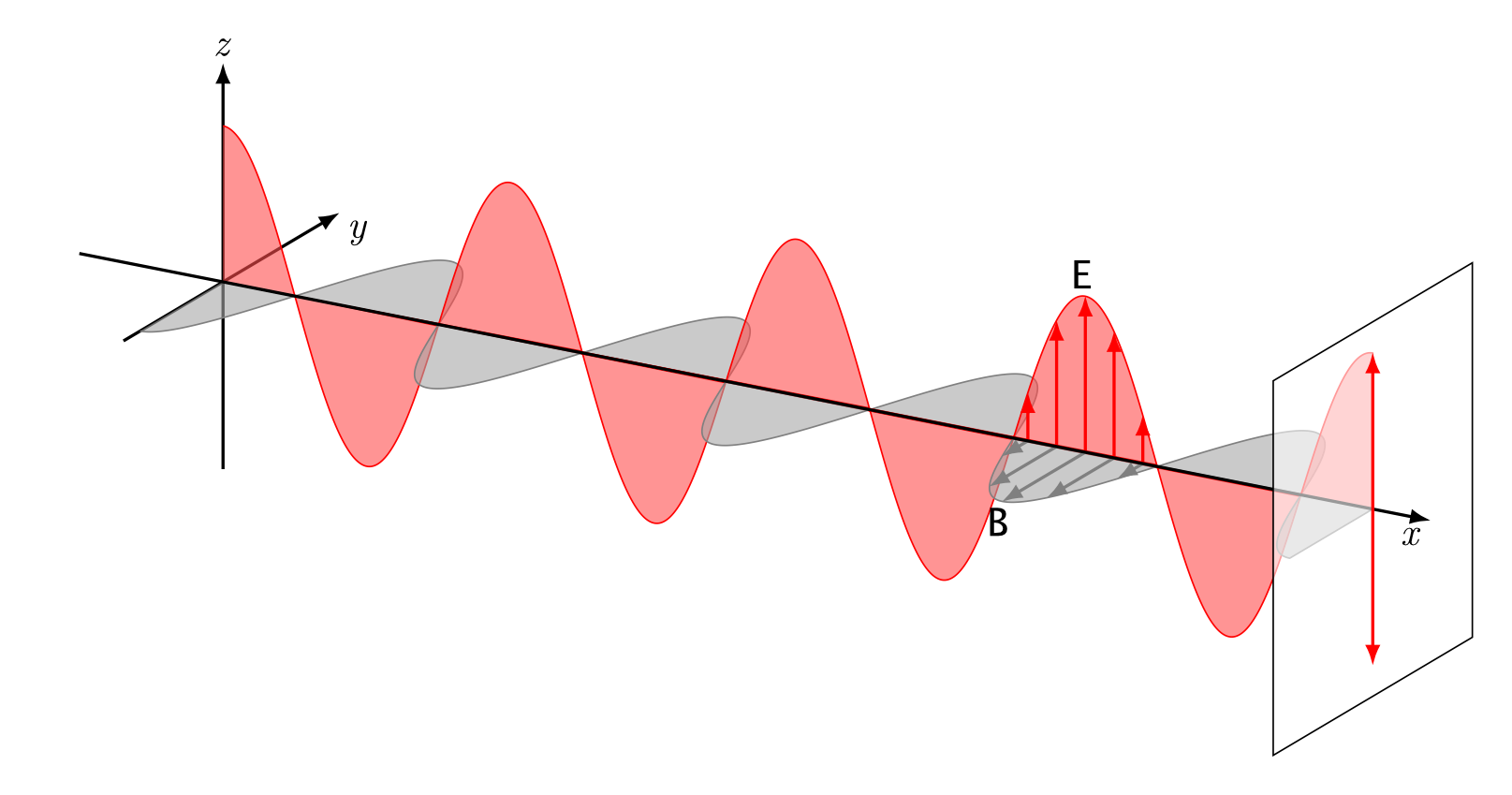
La lumière est une onde électromagnétique, où un champ électrique oscille dans un plan perpendiculaire de celui où oscille le champ magnétique. La direction de propagation de la lumière suit l’intersection de ces deux plans, comme cela est illustré à la figure 1.

La polarisation linéaire de la lumière est définie comme étant la direction selon laquelle son champ électrique oscille. Par exemple, la figure 1 illustre de la lumière polarisée verticalement. La lumière peut également être polarisée circulairement, mais nous n’aborderons pas cette propriété ici.

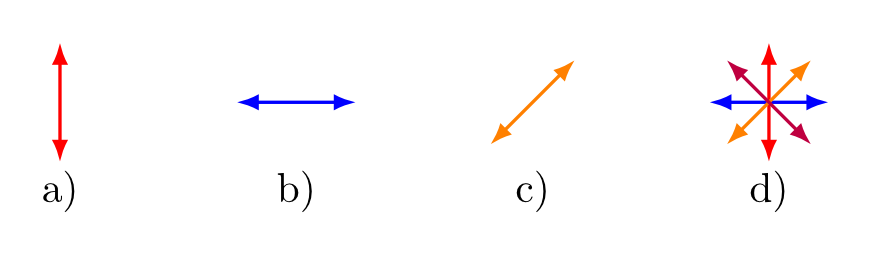
En réalité, tous les photons qui constituent un rayon de lumière ont leurs propres polarisations. Lorsque que ceux-ci ont des polarisations alignées dans la même direction, on dit que la lumière est polarisée linéairement. La lumière peut être polarisée dans toutes les directions : horizontalement, verticalement, diagonalement, et même ne pas être polarisée du tout (voir la figure 2). Dans ce dernier cas, cela signifie que les photons qui constituent cette lumière ont toutes des polarisations qui ne pointent pas dans une direction particulière. La lumière qui nous entoure, comme celle qui nous parvient du soleil, a tendance à ne pas être polarisée.

Filtre polarisant

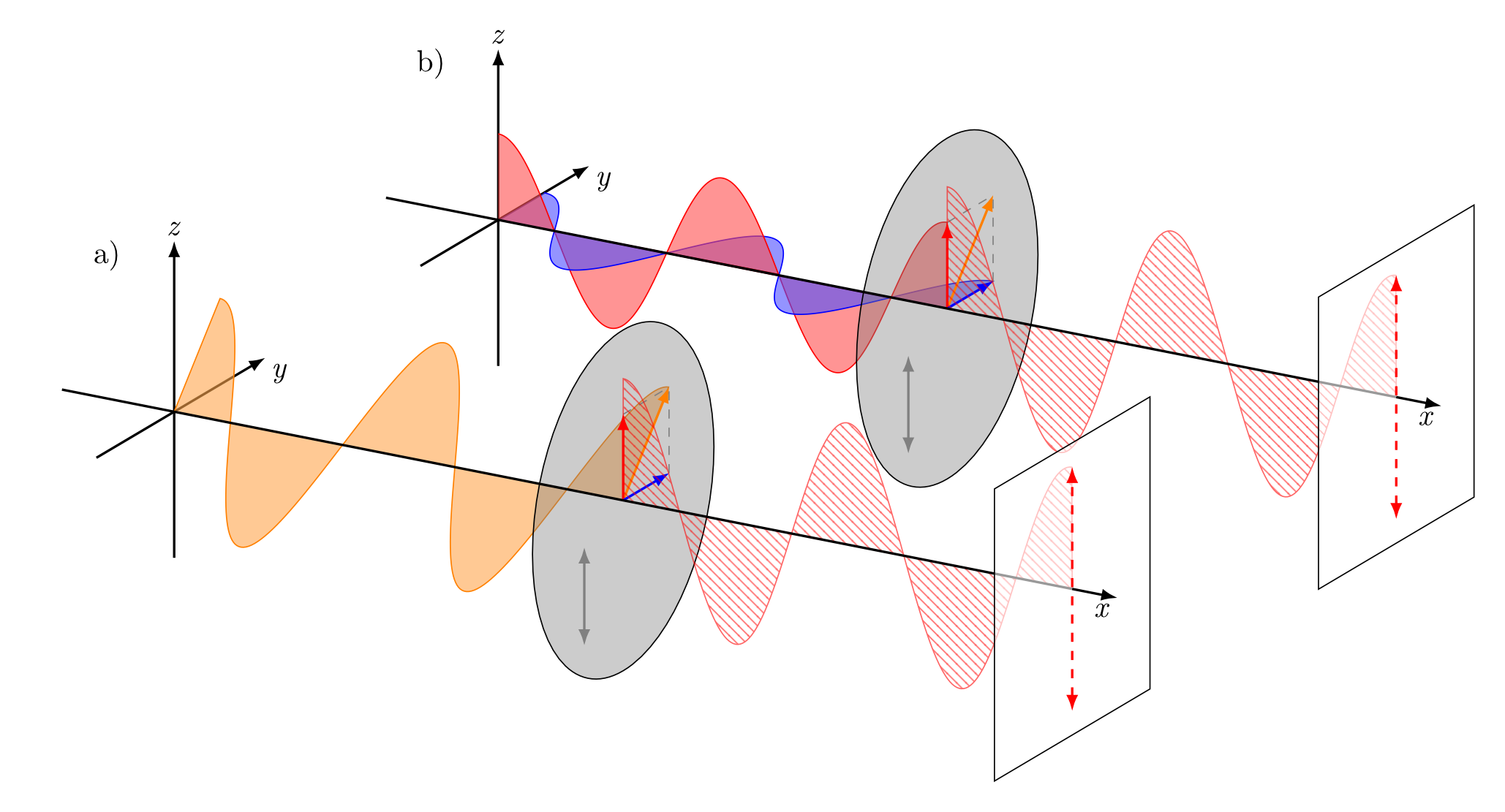
On peut cependant créer de la lumière polarisée, par exemple, en utilisant un filtre polarisant aussi appelé polariseur. La lumière qui réussit à passer à travers un filtre polarisant est nécessairement polarisée dans la direction imposée par l’axe du polariseur. Sur la figure 3, l’axe du polariseur est indiqué par une double flèche grise. On peut voir un tel filtre comme une passoire formée de fentes verticales alors que les photons sont des pièces plates. Seuls les photons dont la polarisation est alignée avec les fentes peuvent passer. Sur la figure 3, le filtre polarisant laisse passer les photons polarisés verticalement (3a) et absorbent les photons polarisés horizontalement (3b). En tournant le filtre polarisant, on tourne par le fait même la polarisation des photons qui peuvent le traverser 3c.

Que se passe-t-il si on envoie un photon avec une polarisation à 45° sur un filtre polarisant qui ne laisse passer que la polarisation verticale? Du point de vue du filtre (figure 4), ce photon est à la fois polarisé verticalement et horizontalement : il est en superposition d’états! Cela est possible car la polarisation est une propriété quantique de la lumière. Ce photon étant en superposition égale des polarisations horizontale et verticale, le filtre doit connaitre sa polarisation pour décider s’il le laisse passer ou non. Pour cela il doit effectivement mesurer l’état de polarisation. Si le photon est mesuré avec une polarisation verticale, il passera complètement à travers le filtre. Cependant, il sera absorbé s’il est mesuré avec une polarisation horizontale.

Sur la figure 4 on représente le fait que ces deux résultats sont possibles avec une onde hachurée : parfois le photon passe, parfois il ne passe pas. Pour une polarisation à 45°, le photon a 50% des chances de passer le filtre. Si cela se produit, il aura alors une polarisation parfaitement verticale. Ensuite, si on modifie l’angle entre la polarisation du photon et du polariseur, les probabilités que le photon passe changeront en suivant la loi de Malus. Et comme c’est quantique, seules les probabilités peuvent être déduites, et le résultat final est tout à fait impossible à prédire!

Que se passe-t-il si on envoie de la lumière qui contient plusieurs photons tous polarisés de la même manière à travers un polariseur? Chacun des photons a la même probabilité de passer le filtre, probabilité qui est donnée par l’angle entre cette polarisation et l’axe du polariseur. Ainsi, la fraction du nombre de photons qui passent est donnée par cette probabilité. L’intensité du faisceau lumineux qui traverse le filtre diminue donc en fonction de l’angle entre la polarisation initiale de la lumière et celle du polariseur.

La superposition : une question de base?

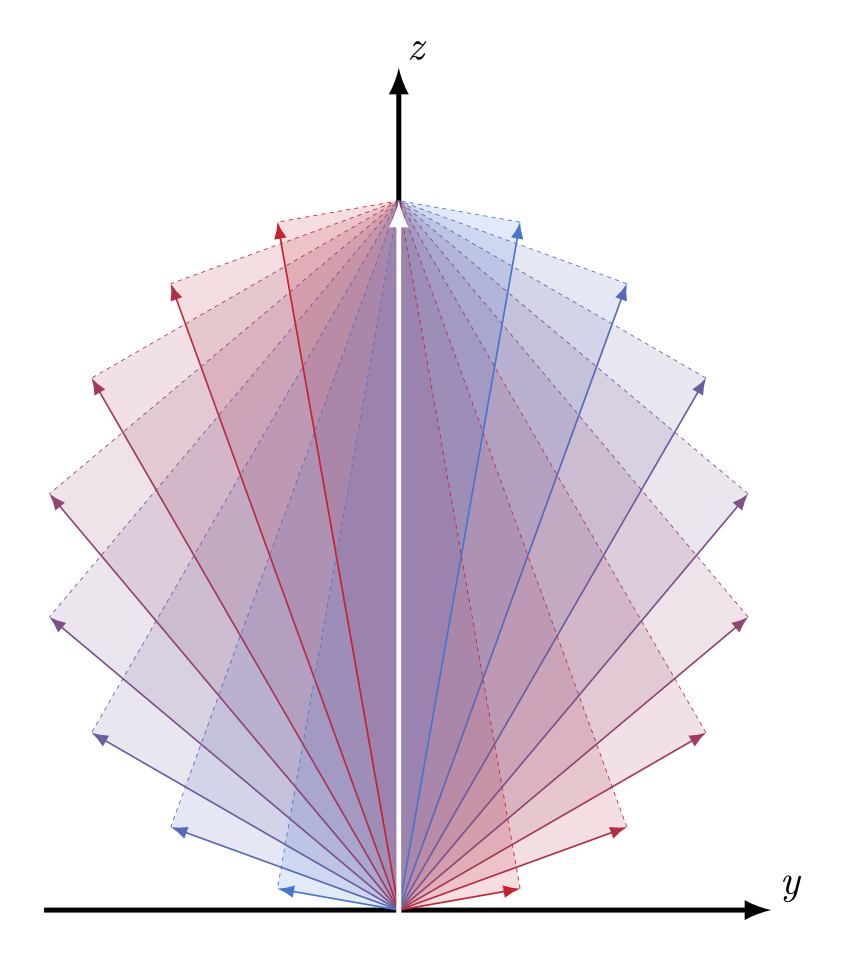
Comme on l’a vu, un photon polarisé linéairement peut apparaitre comme en superposition d’états pour un polariseur dont l’axe n’est pas parallèle ou orthogonal à la polarisation du photon. Cela traduit le fait que la description de la polarisation dépend de la base dans laquelle on la décrit. Sur la figure 5 la polarisation verticale d’un photon (flèche blanche verticale) peut être décomposée dans plusieurs bases différentes. En fonction de cette base, une même polarisation peut être décrite comme étant en superposition ou pas.

Est-ce que la superposition quantique n’est qu’une question de base finalement? Dans le cas de la polarisation c’est effectivement vrai, car les deux polarisations d’une base sont dites dégénérées, l’une n’est pas favorisée par rapport à l’autre, mais ce n’est pas toujours le cas. En effet, si on veut décrire l’état d’un qubit supraconducteur, on peut utiliser la base |0〉, |1〉 ou bien la base |+〉, |-〉. Il est toujours possible de décrire l’état |+〉 comme une superposition de |0〉 et |1〉 ou l’état |0〉 comme une superposition de |+〉 et |-〉. Ce qui distingue la base |0〉, |1〉 de la base |+〉, |-〉 c’est que les deux états de la première base sont caractérisés par des énergies différentes, alors que ce n’est pas le cas de la seconde. Tout ça n’est alors qu’une question de point de vue, l’important c’est de savoir dans quelle base on se trouve!