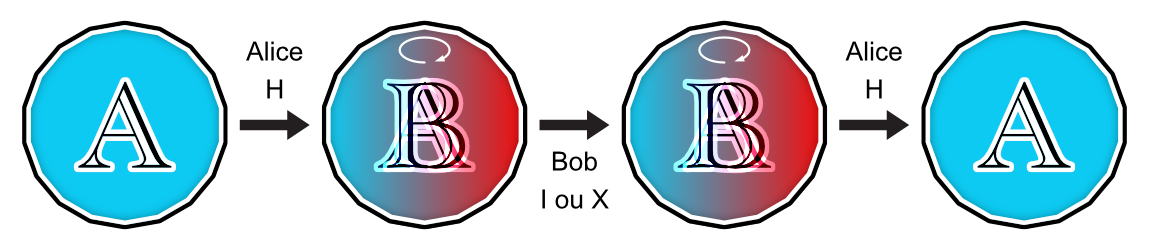Pile ou face quantique
Par Maxime Dion
La mécanique quantique est généralement qualifiée de bizarre et de mystérieuse. En pratique, notre difficulté à appréhender la logique quantique traduit simplement l’absence de phénomènes quantiques dans notre expérience de la réalité. Nous vous proposons ici de vous familiariser avec le phénomène de superposition quantique grâce à un jeu de pile ou face quantique. Le jeu que nous vous présentons a été introduit par Shohini Ghose dans cette conférence TED.
Le jeu
Nos joueurs seront nos deux protagonistes quantiques préférés, Alice et Bob, qui utiliseront une pièce dont les côtés sont identifiés à leurs noms.
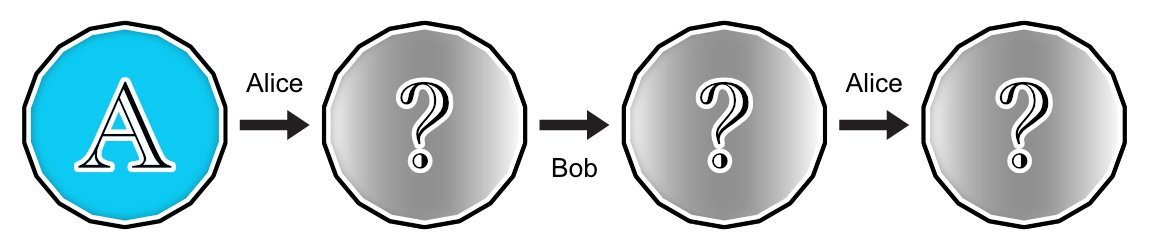
La partie débute avec la pièce placée avec la face A visible par les deux joueurs. Ensuite, cette pièce est cachée. Les joueurs peuvent la retourner, mais sans la voir. Alice joue en premier. Elle a le choix de retourner la pièce ou non, modifiant ainsi son état. À son tour, Bob a la possibilité de retourner la pièce sans connaitre son état. Alice complète la partie en choisissant à nouveau de retourner ou non la pièce. L’état de la pièce est alors révélé. Si la pièce montre la face A à la fin de la partie, Alice gagne. Inversement, Bob gagne la partie si la face B est visible.
Opérations I et X
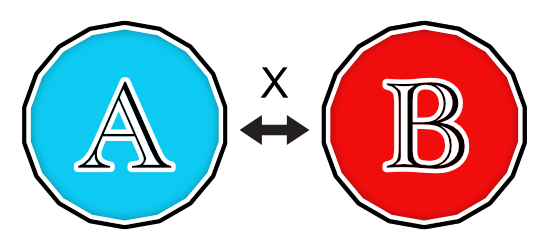
Dans cette version du jeu, Alice et Bob ont accès à deux opérations pour modifier l’état de la pièce. D’abord, s’ils décident de ne pas retourner la pièce, ils appliquent en fait l’opération que l’on appelle identité (ou I). Ensuite, s’ils décident de retourner la pièce, ils ont recours à l’opération « non » (ou X).
Deux utilisations de X ramènent la pièce dans son état initial. On dit donc que cette opération est son propre inverse.
Une partie classique
En utilisant uniquement les opérations I et X, chacun des joueurs a 50% des chances de gagner une manche de ce jeu. Modifions légèrement les règles du jeu en utilisant une pièce quantique! Cela ouvre la possibilité d’utiliser d’autres opérations.
Superposition
Dans la théorie de la mécanique quantique, un objet quantique peut être dans plusieurs états à la fois. On dit alors qu’il est en superposition d’états. Lorsque notre pièce quantique est en superposition d’états, elle montre les faces A et B en même temps.
Bien qu’il n’y ait pas d’équivalent classique à ce phénomène, on peut imaginer qu’une pièce en superposition d’états correspond à une pièce qu’on aurait lancée dans les airs et qui serait en rotation constante autour d’un axe.
Opération H
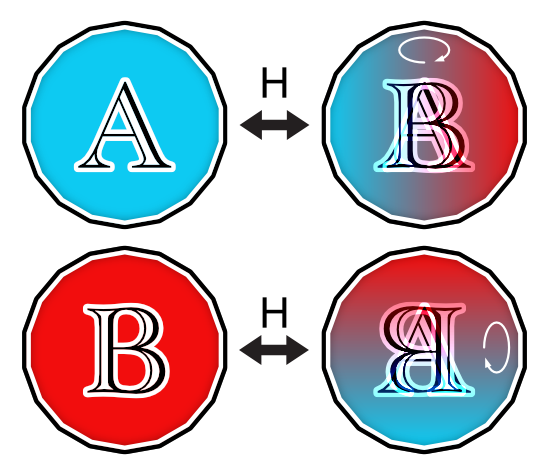
C’est l’opération Hadamard (H) qui permet de placer la pièce en rotation (dans une superposition d’états). Le choix de l’axe dépend de l’état initial de la pièce. Si la pièce était sur la face A (B) initialement, l’axe de rotation sera vertical (horizontal). On représente la direction de cet axe par l’orientation des lettres A et B et du dégradé de couleurs.
Toutefois, cette rotation est bien particulière, car l’opération H est son propre inverse : on peut arrêter la rotation en appliquant H une seconde fois. Par exemple, l’application de H sur la pièce en rotation autour de l’axe vertical (horizontal) la ramène dans l’état A (B).
Ce n’est pas de la triche, c’est quantique!
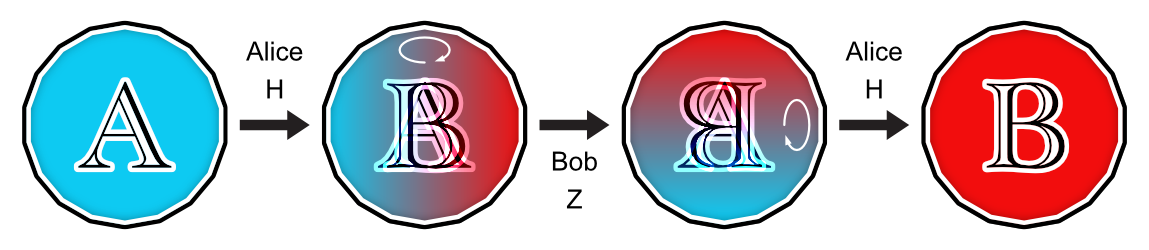
Alice est la première à saisir l’opportunité offerte par la quantique et décide d’utiliser l’opération Hadamard pour modifier l’état de la pièce durant ses deux tours. Bob n’a pas saisi les possibilités que la quantique offre et continue de jouer en utilisant seulement I ou X. Voici comment se déroule la première partie quantique… et toutes les suivantes!
Alice gagne maintenant à tous les coups, peu importe ce que Bob joue! En effet, l’opération X échange les faces A et B, mais lorsque la pièce est en superposition d’état, cela ne change rien : l’effet est le même que I. Bob doit changer sa stratégie!
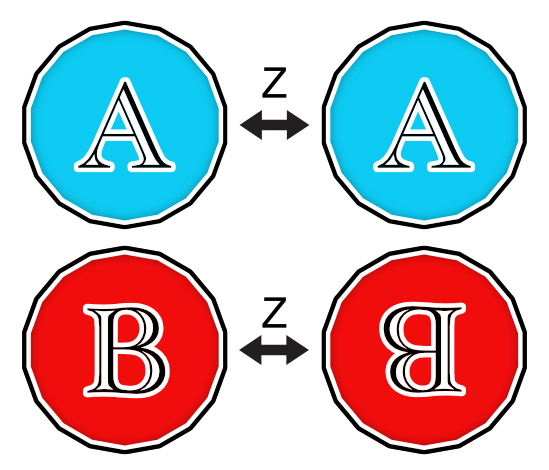
Opération Z
Bob découvre l’opération Z. Celle-ci n’affecte pas la pièce lorsqu’elle est du côté A, mais tourne la pièce de 180° lorsqu’elle est du côté B.
Cela ne semble pas particulièrement quantique! Néanmoins, Bob décide de jouer cette opération durant son tour, car il constate que si la pièce est en superposition d’états, cela changera l’axe de rotation de la pièce. Si on retourne voir l’effet qu’a l’opération H sur la pièce qui tourne autour de l’axe horizontal, on voit que la pièce sera sur la face B à la fin de la partie si Alice joue H à son deuxième tour.
Si Alice continue de jouer uniquement des opérations H, Bob est alors assuré de gagner! Alice devra réajuster sa stratégie en utilisant parfois l’opération H et parfois X pour pouvoir gagner. Dans tous les cas, les chances seront à nouveau de 50% de l’emporter pour chaque joueur, tout le monde jouant à armes égales!